Learn to Invest Money - The Power of Compound Interests
When you will learn to invest money you will discover the magic of compound interest, when interest is added to the principal, so that interest itself earns interest.
When you will learn to invest money you should specifically focus on the secret of saving, this is the power of compound interest. Compound interest is the payment of interest on both principal as well past accrued interest. This addition of interest to the principal is called compounding.
When you're saving, the bank (or financial institution) adds interest to your savings at regular intervals (for example, every month). If you don't touch the interest, but let it add to your lump sum, then you start to earn interest on your interest, as well as on the original amount you saved.
The longer you leave your money, the more powerful the compound interest effect. So the earlier you start saving, the more you make from compound interest. The same applies to other investments such as shares, where you regularly reinvest dividends, or the company reinvests its profits.
Where compound interest is applied, the investment grows exponentially and not linearly as in the case of simple interest.
Learn to Invest Money - Compound Interest Formula
Learn To Invest Money - Compound Interest Calculator
Please enter the required data and calculate your saved amount if you would invest an amount of money (principal) today at specified interest rate (interest rate) and you would leave it at the bank for predefined number of years (conversion periods).
Calculator only works if you enter correct data in textboxes bellow. Please use (dot) '.' as decimal point in interest rate data field and enter interest rate in the following format 0.01 (in case interest rate is equal to 1%).
S = P*(1+i)^n
Where:
- S = Saved amount (principal + interest)
- P = Principal
- i = Interest rate per conversion period
- n = Total number of conversion periods
In order to define an interest rate fully, and enable one to compare it with other interest rates, the interest rate and the compounding frequency must be disclosed. The more frequently interest is added to the principal, the faster the principal grows and the higher the compound interest will be. The longer the time period the greater the effect of compounding.
Learn To Invest Money - Compound Interest Example
If you would invest $100,000 for five years at an interest rate of 5% compounded quarterly, you would earn $28,203.72 as interest.
- P = $100,000
- i = 0.05 / 4, or 0.0125
- n = 4 * 5, or 20, conversion periods over the five years
Therefore, the saved amount, S, is:
S = $100,000*(1 + 0.0125)^20 = $100,000 x 1.282037 = $128,203.72
Compound interest is standard in finance and economics, and simple interest is used infrequently (although certain financial products may contain elements of simple interest). You must understand the concept of compound interest if you would like to learn to invest money further.
Learn to Invest Money - Compound vs. Simple Interests
Compound interest may be contrasted with simple interest, where interest is not added to the principal (there is no compounding).
Without compound interest a $1,000 savings account at 10% per year earns a flat $100 in interest each year. After 10 years that non compound interest savings account is worth $2,000. With compound interest that same $1,000 savings account earns $100 in interest the first year, but earns increasing amounts of interest in each subsequent year. The reason is that with compound interest, interest is paid on the previous years' interest. After 10 years our $1,000 savings account with compound interest is worth more than $2,593, which is $593 more than simple interest calculation.
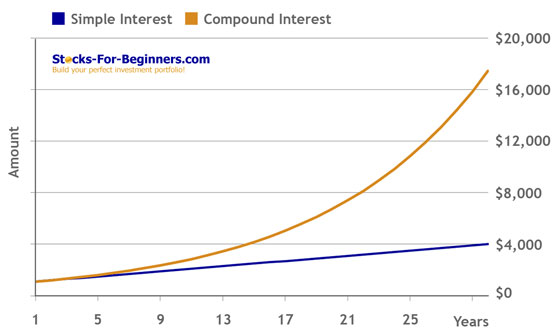
| Year | Simple Interest | Simple Amount | Compound Interest | Compound Amount |
|---|---|---|---|---|
| 1 | $100 | $1,100 | $100 | $1,100 |
| 2 | $100 | $1,200 | $110 | $1,210 |
| 3 | $100 | $1,300 | $121 | $1,331 |
| 4 | $100 | $1,400 | $133 | $1,464 |
| 5 | $100 | $1,500 | $146 | $1,611 |
| 6 | $100 | $1,600 | $161 | $1,772 |
| 7 | $100 | $1,700 | $177 | $1,949 |
| 8 | $100 | $1,800 | $195 | $2,144 |
| 9 | $100 | $1,900 | $214 | $2,358 |
| 10 | $100 | $2,000 | $236 | $2,594 |
| 11 | $100 | $2,100 | $259 | $2,853 |
| 12 | $100 | $2,200 | $285 | $3,138 |
| 13 | $100 | $2,300 | $314 | $3,452 |
| 14 | $100 | $2,400 | $345 | $3,797 |
| 15 | $100 | $2,500 | $380 | $4,177 |
| 16 | $100 | $2,600 | $418 | $4,595 |
| 17 | $100 | $2,700 | $459 | $5,054 |
| 18 | $100 | $2,800 | $505 | $5,560 |
| 19 | $100 | $2,900 | $556 | $6,116 |
| 20 | $100 | $3,000 | $612 | $6,727 |
| 21 | $100 | $3,100 | $673 | $7,400 |
| 22 | $100 | $3,200 | $740 | $8,140 |
| 23 | $100 | $3,300 | $814 | $8,954 |
| 24 | $100 | $3,400 | $895 | $9,850 |
| 25 | $100 | $3,500 | $985 | $10,835 |
| 26 | $100 | $3,600 | $1,083 | $11,918 |
| 27 | $100 | $3,700 | $1,192 | $13,110 |
| 28 | $100 | $3,800 | $1,311 | $14,421 |
| 29 | $100 | $3,900 | $1,442 | $15,863 |
| 30 | $100 | $4,000 | $1,586 | $17,449 |
Learn to Invest Money - Annual Percentage Rate
Since most people prefer to think of rates as a yearly percentage, many governments require financial institutions to disclose the equivalent yearly compounded interest rate on deposits or advances. For instance the yearly rate for a loan with 1% interest per month is approximately 12.68% per annum (1.01^12). This equivalent yearly rate may be referred to as annual percentage rate (APR).
Written by: Goran Dolenc
Do you find this content useful? Like! Tweet! Recommend! Share!
Back from Learn to Invest Money to How to Invest in Stock
Back from Learn to Invest Money to Best Online Trading Site for Beginners home page

























































